The Contributions of Andrew Wiles to Number Theory
Andrew Wiles, a name synonymous with one of the greatest achievements in mathematics, has left an indelible mark on number theory through his groundbreaking proof of Fermat's Last Theorem. For over three centuries, this theorem stood as a formidable challenge, capturing the imaginations of mathematicians and enthusiasts alike. Wiles's journey to proving this theorem is not just a tale of persistence; it's a narrative filled with passion, intellectual curiosity, and an unwavering commitment to uncovering the truths hidden within the fabric of numbers.
Fermat's Last Theorem posits that there are no three positive integers \(a\), \(b\), and \(c\) that satisfy the equation \(a^n + b^n c^n\) for any integer value of \(n\) greater than 2. This deceptively simple statement, scribbled in the margin of a book by Pierre de Fermat in 1637, sparked centuries of mathematical exploration and debate. The theorem became a beacon for mathematicians, drawing them into a complex world of algebra, geometry, and number theory, yet remained unproven until Wiles's remarkable achievement in the 1990s. His proof not only resolved a historical enigma but also revolutionized the field of mathematics, intertwining various branches of the discipline in ways that had never been seen before.
Wiles's contributions extend beyond the theorem itself; they serve as a testament to the power of human ingenuity and the relentless pursuit of knowledge. His work has inspired countless mathematicians to delve deeper into number theory, exploring the intricate connections between different mathematical concepts. The implications of his proof have paved the way for new research avenues, creating a ripple effect that continues to influence modern mathematics.
In essence, Andrew Wiles's contributions to number theory exemplify the beauty and complexity of mathematics. His journey from a young boy captivated by numbers to a leading figure in mathematical history is a powerful reminder that the pursuit of knowledge is often fraught with challenges, yet it is through these challenges that we uncover the most profound truths. The legacy of Wiles's work will undoubtedly inspire future generations to push the boundaries of mathematical understanding, proving that even the most daunting problems can be solved with determination and creativity.
- What is Fermat's Last Theorem?
Fermat's Last Theorem states that there are no three positive integers \(a\), \(b\), and \(c\) that satisfy the equation \(a^n + b^n c^n\) for any integer value of \(n\) greater than 2.
- How long did it take Andrew Wiles to prove the theorem?
Wiles worked in secrecy for about seven years before announcing his proof in 1994, and it took an additional year to resolve a gap in the proof that was identified by his peers.
- What impact did Wiles's proof have on mathematics?
Wiles's proof not only solved a centuries-old problem but also introduced new techniques that have influenced various areas of mathematics, particularly in number theory and algebraic geometry.

Fermat's Last Theorem
is one of the most famous problems in the history of mathematics, capturing the imagination of mathematicians and enthusiasts alike for over 350 years. The theorem states that there are no three positive integers \(a\), \(b\), and \(c\) that can satisfy the equation \(a^n + b^n c^n\) for any integer value of \(n\) greater than 2. This deceptively simple statement, scribbled in the margin of a book by Pierre de Fermat in 1637, ignited a quest that would span generations and lead to profound developments in number theory.
The historical significance of Fermat's Last Theorem cannot be overstated. It stood as a challenge to some of the greatest minds in mathematics, including Leonhard Euler, Joseph-Louis Lagrange, and Andrew Wiles himself. Each of these mathematicians made significant contributions to the understanding of numbers, yet Fermat's assertion remained unproven, leading many to believe it was simply an unassailable mystery. The theorem became a symbol of mathematical intrigue, inspiring countless mathematicians to attempt to prove or disprove it over the centuries.
Imagine a grand puzzle that has tantalized intellectuals for centuries; this is how many viewed Fermat's Last Theorem. The theorem was not just a statement about numbers; it represented a deeper philosophical question about the nature of proof and the limits of mathematical understanding. It was as if Fermat had thrown down a gauntlet, challenging mathematicians to delve into the depths of number theory and explore the very fabric of mathematics itself.
Throughout its history, the theorem has undergone various attempts at proof, with mathematicians developing increasingly sophisticated tools and theories. For instance, in the 19th century, mathematicians like Évariste Galois and Henri Poincaré contributed to the field of algebraic structures, which would later play a crucial role in Wiles's eventual proof. The journey to solving Fermat's Last Theorem was not merely about finding a solution but involved a rich tapestry of mathematical innovation and collaboration.
Finally, in the 1990s, Andrew Wiles emerged as the mathematician who would conquer this centuries-old enigma. His proof, which utilized concepts from elliptic curves and modular forms, not only resolved Fermat's Last Theorem but also opened new avenues in number theory, demonstrating the interconnectedness of various mathematical domains. Wiles's work stands as a testament to the power of perseverance and creativity in the face of seemingly insurmountable challenges.
In summary, Fermat's Last Theorem is more than just a statement about integers; it is a profound narrative of human curiosity, intellectual struggle, and triumph. The theorem's legacy continues to inspire mathematicians, reminding us that even the simplest questions can lead to the most complex and beautiful discoveries.

Wiles's Early Life
Andrew Wiles was born on April 11, 1953, in Cambridge, England, into a family that fostered a love for learning and intellectual curiosity. From a young age, he exhibited a deep fascination with numbers and patterns, often finding himself lost in the world of mathematics. This early passion was not merely a fleeting interest; it was a defining characteristic of his childhood. Wiles's parents encouraged his academic pursuits, providing him with the resources and support that would lay the foundation for his future achievements.
During his formative years, Wiles attended the prestigious King's College School in Cambridge, where he was exposed to a variety of subjects. However, it was mathematics that captivated him the most. He recalls being particularly inspired by a moment in his childhood when he first encountered Fermat's Last Theorem. The theorem, which states that no three positive integers \(a\), \(b\), and \(c\) can satisfy the equation \(a^n + b^n c^n\) for any integer value of \(n\) greater than two, sparked a fire in Wiles's imagination. He later described this moment as a pivotal point in his life, one that ignited his lifelong quest to solve this enigma.
Wiles's academic journey continued at Oxford University, where he pursued his undergraduate studies in mathematics. Here, he was surrounded by brilliant minds and was deeply influenced by his professors and peers. His thirst for knowledge led him to delve into various mathematical fields, but he always returned to number theory, the area that would ultimately define his career. After completing his degree, Wiles went on to earn his Ph.D. from the University of Cambridge in 1975, where he began to develop the skills and insights that would later prove crucial in his groundbreaking work.
Throughout his education, Wiles faced numerous challenges, but his determination never wavered. He often spent countless hours poring over mathematical texts, driven by an insatiable curiosity and a desire to understand the complexities of the universe through numbers. It was during this period of intense study that Wiles began to formulate the ideas that would eventually lead him to his monumental proof of Fermat's Last Theorem.
In addition to his academic pursuits, Wiles's early life was also marked by significant mentorship. He was fortunate to have several influential figures in his life, including his thesis advisor, who recognized his potential and encouraged him to think critically about mathematical problems. This mentorship played a crucial role in shaping Wiles's approach to mathematics and helped him cultivate the resilience needed to tackle the formidable challenges that lay ahead.
To sum up, Andrew Wiles's early life was characterized by a unique blend of curiosity, determination, and support from his family and mentors. These elements combined to create a fertile ground for his mathematical genius to flourish, setting the stage for his future accomplishments in number theory. Wiles's journey from a curious child to a world-renowned mathematician serves as a testament to the power of passion and perseverance in the pursuit of knowledge.
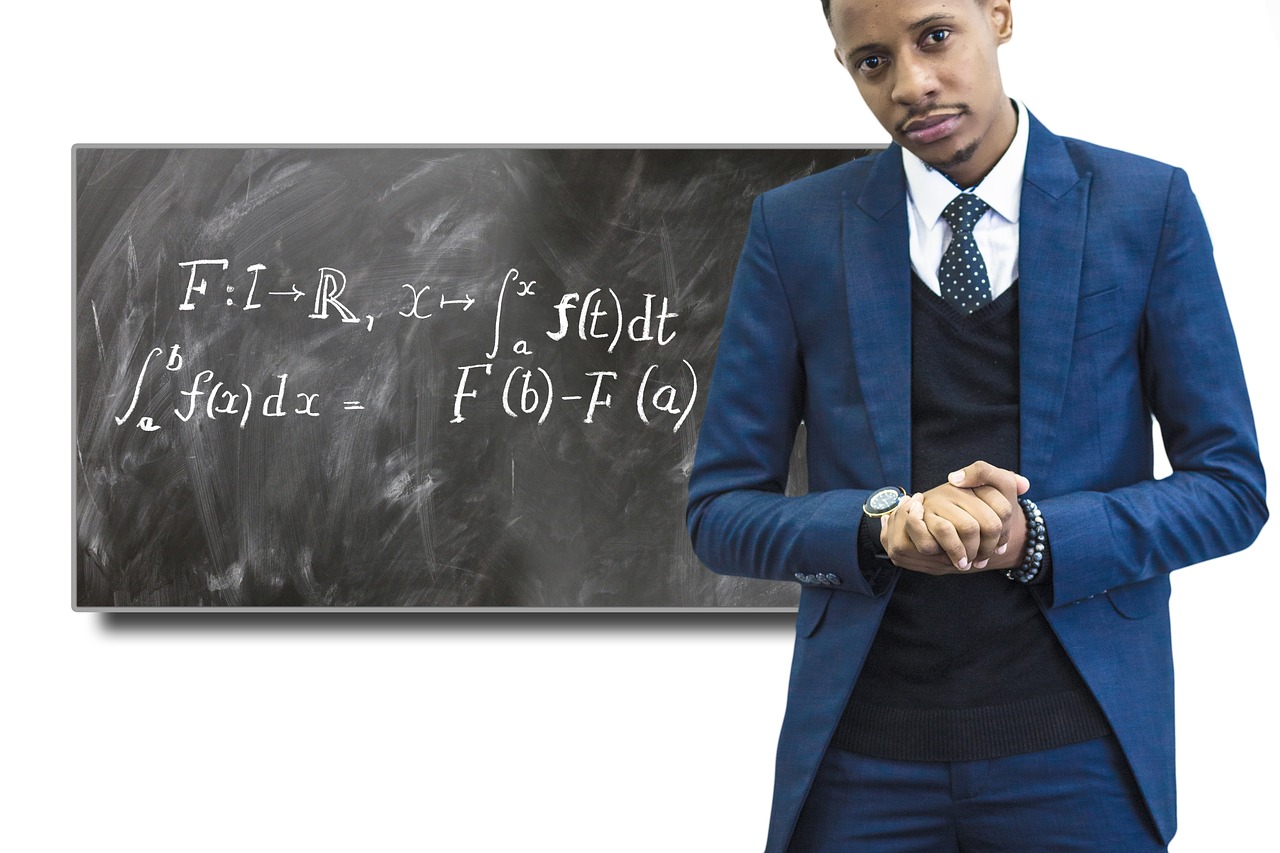
The Journey to the Proof
The journey to proving Fermat's Last Theorem was nothing short of a mathematical odyssey for Andrew Wiles. It all began as a childhood fascination that blossomed into a lifelong obsession. Imagine a young boy, captivated by the idea that a simple equation could hold secrets that stumped the greatest minds for centuries. This was Wiles, who, at the tender age of 10, stumbled upon Fermat's enigmatic claim in a library book. Little did he know, this moment was the spark that would ignite a relentless pursuit of knowledge and understanding.
Wiles's quest was not just a matter of crunching numbers and scribbling equations; it was a profound journey filled with intellectual challenges and emotional highs and lows. He dedicated nearly a decade of his life to this singular goal, working in isolation in his attic office at Princeton University. This solitude was both a blessing and a curse. On one hand, it allowed him to dive deep into the complexities of number theory without distractions; on the other hand, it could be incredibly isolating. As he immersed himself in the intricacies of mathematical theory, he faced numerous obstacles that would have deterred most. Yet, Wiles pressed on, driven by an unwavering belief in his ability to unravel the mystery.
Initially, Wiles attempted to prove the theorem using various techniques he had learned throughout his studies. However, each attempt revealed new layers of complexity and highlighted the limitations of existing mathematical tools. His early trials were marked by frustration, as he encountered setbacks that forced him to rethink his approach. He realized that to succeed, he would need to venture into uncharted territory, leveraging concepts from different areas of mathematics. This realization marked a turning point in his journey.
One of the most significant aspects of Wiles's journey was the collaboration and mentorship he sought along the way. While he worked largely in isolation, he also reached out to fellow mathematicians, forming connections that would prove invaluable. These relationships not only provided him with fresh perspectives but also offered a support network that encouraged him to persevere during tough times. It was through these interactions that he began to understand the profound connections between elliptic curves and modular forms, which would ultimately play a crucial role in his proof.
As Wiles neared the conclusion of his work, he faced a critical moment that tested his resolve. After presenting his proof in 1993, a flaw was discovered, sending shockwaves through the mathematical community. Instead of succumbing to despair, Wiles took this setback as an opportunity to deepen his understanding and refine his approach. With the help of his former student, Richard Taylor, he worked tirelessly to correct the error. This collaboration not only strengthened his proof but also exemplified the power of teamwork in the world of mathematics.
Finally, in 1994, after years of relentless effort, Wiles announced a complete and correct proof of Fermat's Last Theorem. The mathematical community erupted in applause, and Wiles became a symbol of perseverance and dedication. His journey was a testament to the idea that great achievements often stem from years of hard work, relentless curiosity, and the courage to face challenges head-on. This monumental moment not only changed Wiles's life but also reshaped the landscape of number theory, inspiring future generations of mathematicians to pursue the mysteries that lie within the world of numbers.

Initial Attempts
Andrew Wiles's journey to proving Fermat's Last Theorem was anything but straightforward. In fact, it was a winding road filled with that often led to frustration and setbacks. Wiles first encountered the theorem as a young boy, and from that moment, it became a burning passion for him. However, the road to a definitive proof was littered with challenges that would test his resolve and intellect.
Initially, Wiles approached the theorem through various mathematical lenses, attempting to connect it with different areas of number theory. He spent years exploring the realms of elliptic curves and modular forms, both of which would later play crucial roles in his eventual proof. However, during these early attempts, he faced significant obstacles:
- Complexity of the Theorem: The theorem itself is deceptively simple to state but incredibly complex in its implications. Wiles often felt overwhelmed by the depth of the problem.
- Lack of Progress: For several years, Wiles struggled to make any substantial progress. His early attempts yielded little more than a deeper understanding of the theorem's intricacies.
- Isolation: Wiles chose to work in relative solitude, away from the academic community. While this allowed him to focus, it also meant he had fewer opportunities for feedback and collaboration.
Despite these hurdles, Wiles's determination never wavered. He would often spend long nights immersed in his work, driven by the dream of solving a problem that had stumped mathematicians for over 350 years. He likened his experience to climbing a mountain, where each false summit only fueled his desire to reach the peak. It was during these formative years of struggle that Wiles honed his skills and developed the innovative thinking that would eventually lead to his breakthrough.
As he delved deeper into his research, Wiles began to see connections between previously unrelated areas of mathematics. This realization was akin to discovering hidden pathways on a well-trodden trail. Each new insight brought him closer to the elusive proof, and while the journey was fraught with difficulties, it ultimately laid the groundwork for one of the most significant achievements in modern mathematics.
In retrospect, Wiles's initial attempts were not merely failures; they were essential steps in a larger process of discovery. Each setback provided valuable lessons that shaped his approach and refined his methods. It was through this arduous journey that Wiles transformed from a passionate mathematician into a pioneering figure in number theory, ready to tackle the monumental task ahead of him.

Collaboration and Mentorship
Throughout his illustrious career, Andrew Wiles has often emphasized the pivotal role that collaboration and mentorship played in his journey to proving Fermat's Last Theorem. Mathematics, while often perceived as a solitary pursuit, is deeply enriched by the interactions and exchanges between scholars. Wiles's experience is a perfect testament to this. From his early days as a budding mathematician, he sought guidance and inspiration from established figures in the field, which helped shape his understanding and approach toward complex problems.
One of the most significant influences on Wiles was his time at the University of Cambridge, where he was exposed to a vibrant mathematical community. Here, he had the opportunity to collaborate with other mathematicians, sharing ideas and tackling challenging concepts together. This environment fostered a sense of camaraderie and support, allowing Wiles to refine his thoughts and strategies. Moreover, the mentorship he received from renowned mathematicians was crucial. For instance, he often credits his advisor, Sir Michael Atiyah, as a key figure who not only provided guidance but also encouraged him to pursue his passion for number theory relentlessly.
Wiles's journey was not devoid of challenges. During his years of research, he faced numerous setbacks and moments of self-doubt. However, the support from his peers and mentors helped him navigate these turbulent waters. They provided not just intellectual support but also a sense of community that reassured him he was not alone in his quest. In a field where ideas can take years, if not decades, to mature, having a network of collaborators is invaluable.
Additionally, Wiles has been an advocate for the importance of mentorship in mathematics. He believes that fostering the next generation of mathematicians is essential for the continued advancement of the field. He has actively participated in mentoring young mathematicians, sharing his insights and experiences, and encouraging them to think outside the box. This cycle of mentorship not only benefits the mentees but also enriches the mathematical community as a whole.
To illustrate the impact of collaboration and mentorship in Wiles's journey, consider the following table that outlines some key figures who influenced his work:
| Name | Role | Contribution |
|---|---|---|
| Sir Michael Atiyah | Advisor | Guided Wiles in his early academic pursuits and encouraged his interest in number theory. |
| Gerd Faltings | Peer | His work on the theorem of Faltings inspired Wiles and helped shape his approach to the proof. |
| Richard Taylor | Collaborator | Worked closely with Wiles to resolve issues in the proof, particularly during the final stages. |
In conclusion, the journey to proving Fermat's Last Theorem was not a solitary one for Andrew Wiles. It was a path paved with the invaluable contributions of mentors and collaborators who shaped his mathematical journey. The relationships he built during his formative years and throughout his career not only aided his monumental achievement but also reinforced the notion that mathematics thrives on collaboration.
- What is Fermat's Last Theorem? It states that there are no three positive integers a, b, and c that satisfy the equation a^n + b^n c^n for any integer value of n greater than 2.
- How long did it take Wiles to prove the theorem? Wiles worked on the proof for nearly seven years before he announced it in 1994.
- What are elliptic curves and modular forms? These are advanced mathematical concepts that Wiles used in his proof. Elliptic curves are algebraic curves that have certain properties, while modular forms are complex functions that are symmetrical in nature.
- What impact did Wiles's proof have on mathematics? It not only solved a centuries-old problem but also opened new avenues of research in number theory and related fields.

Mathematical Techniques Used
When Andrew Wiles set out to prove Fermat's Last Theorem, he employed a remarkable array of mathematical techniques that not only showcased his genius but also revolutionized the field of number theory. At the heart of his proof lies the intricate relationship between elliptic curves and modular forms. These two concepts were pivotal in his approach, and understanding them is key to grasping the brilliance of Wiles's work.
To put it simply, elliptic curves can be thought of as smooth, donut-shaped graphs defined by cubic equations. They have unique properties that allow mathematicians to explore deep connections with number theory. Modular forms, on the other hand, are complex functions that exhibit a certain level of symmetry and can be considered as "building blocks" in the realm of mathematics. Wiles's groundbreaking insight was to demonstrate that every elliptic curve is, in fact, associated with a modular form. This connection, known as the Taniyama-Shimura-Weil Conjecture, was the linchpin of his proof.
Wiles's journey to prove this conjecture was fraught with challenges. He meticulously constructed a framework that linked these two seemingly disparate areas of mathematics. By establishing this relationship, he was able to leverage the properties of modular forms to draw conclusions about elliptic curves, ultimately leading to the proof of Fermat's Last Theorem. This was no small feat; it required not only a deep understanding of both fields but also an innovative approach to problem-solving.
In addition to elliptic curves and modular forms, Wiles also utilized techniques from Galois theory and algebraic geometry. Galois theory, which studies symmetries in the roots of polynomial equations, provided Wiles with essential tools to analyze the properties of the equations he was working with. Algebraic geometry, on the other hand, allowed him to visualize and manipulate the geometric aspects of the curves and forms involved in his proof. The interplay of these mathematical disciplines created a rich tapestry of ideas that Wiles wove together to achieve his historic breakthrough.
Moreover, Wiles's proof was not merely a solitary endeavor; it was built upon the shoulders of giants. He drew heavily from the work of mathematicians who came before him, including Gerard Frey and Jean-Pierre Serre, whose contributions laid the groundwork for Wiles's own discoveries. This collaborative spirit in mathematics is vital, as it highlights how ideas evolve and grow through shared knowledge and inquiry.
In summary, the mathematical techniques employed by Andrew Wiles in his proof of Fermat's Last Theorem were a sophisticated blend of various fields, including elliptic curves, modular forms, Galois theory, and algebraic geometry. His ability to connect these diverse concepts not only solved a centuries-old problem but also opened new avenues for research and exploration in number theory. Wiles's work serves as a testament to the power of innovative thinking and collaboration in mathematics.
- What is Fermat's Last Theorem?
Fermat's Last Theorem states that there are no three positive integers a, b, and c that satisfy the equation a^n + b^n c^n for any integer value of n greater than 2. - How did Wiles prove the theorem?
Wiles proved the theorem by establishing a connection between elliptic curves and modular forms, ultimately demonstrating that the Taniyama-Shimura-Weil Conjecture held true for a specific class of elliptic curves. - Why are elliptic curves important?
Elliptic curves are important because they have profound implications in number theory and cryptography, and they serve as a bridge between different areas of mathematics. - What recognition has Wiles received for his work?
Andrew Wiles has received numerous awards, including the Abel Prize in 2016 and the Clay Millennium Prize for his proof of Fermat's Last Theorem.

Impact on Number Theory
Andrew Wiles's monumental proof of Fermat's Last Theorem didn't just solve a centuries-old puzzle; it ignited a revolution in the field of number theory. Imagine a massive dam holding back a river of mathematical inquiry. For over 350 years, that dam held strong against the relentless flow of curiosity and ambition surrounding Fermat's Last Theorem. Wiles's proof was like the dynamite that finally broke through, unleashing a torrent of new ideas, techniques, and research that reshaped the landscape of mathematics.
Before Wiles, the theorem was a tantalizing enigma, attracting the attention of some of the greatest mathematical minds. The failure to prove it left many mathematicians scratching their heads and questioning the very foundations of number theory. However, Wiles’s success not only confirmed the theorem but also revealed deep connections between seemingly unrelated areas of mathematics, such as elliptic curves and modular forms. This breakthrough has had profound implications, leading to new questions and explorations that continue to this day.
One of the most significant impacts of Wiles's work is the way it has opened new avenues for research in number theory. The techniques he developed and the concepts he explored have become fundamental tools for mathematicians. For instance, the relationship between elliptic curves and modular forms, which Wiles utilized, has led to a surge in research focused on these areas. Many mathematicians are now investigating how these connections can be applied to other unsolved problems, thus expanding the horizons of number theory.
Moreover, Wiles's achievement has inspired a new generation of mathematicians. Young scholars, energized by his story and the implications of his work, are diving into number theory with renewed passion. The excitement surrounding Wiles's proof has created a vibrant community dedicated to exploring the depths of mathematical theory. This is not just a ripple effect; it's a full-blown wave of enthusiasm that is revitalizing the field.
To illustrate the impact of Wiles's proof, consider the following table that summarizes some key areas of research that have emerged as a direct consequence:
| Research Area | Description | Notable Contributions |
|---|---|---|
| Elliptic Curves | Investigating properties and applications of elliptic curves in number theory. | New algorithms for integer factorization. |
| Modular Forms | Studying the structure and behavior of modular forms and their connections to number theory. | Advancements in the Langlands program. |
| Arithmetic Geometry | Exploring the interplay between algebraic geometry and number theory. | Development of new techniques in Diophantine equations. |
In addition to inspiring research, Wiles's proof has also led to increased collaboration among mathematicians. The complexity of the ideas involved has encouraged experts from various fields to come together, sharing insights and fostering a collaborative spirit that was perhaps less prevalent before. This collaborative environment is essential for tackling the challenging problems that lie ahead.
Ultimately, Wiles's contributions to number theory extend far beyond his proof of Fermat's Last Theorem. He has reshaped our understanding of mathematical relationships, inspired countless mathematicians, and opened new pathways for exploration. The impact of his work will echo through the halls of mathematics for generations to come, proving that sometimes, a single breakthrough can change the entire course of a field.
- What is Fermat's Last Theorem? Fermat's Last Theorem states that there are no three positive integers a, b, and c that satisfy the equation a^n + b^n c^n for any integer value of n greater than 2.
- Why was Wiles's proof significant? Wiles's proof was significant because it resolved a long-standing mathematical problem and established new connections between different areas of mathematics.
- What are elliptic curves? Elliptic curves are a type of smooth, projective algebraic curve that have important applications in number theory and cryptography.
- How has Wiles influenced modern mathematics? Wiles's work has inspired a new generation of researchers, led to advancements in number theory, and fostered collaboration among mathematicians across various disciplines.

Further Research Inspired by Wiles
Andrew Wiles's proof of Fermat's Last Theorem didn't just close the book on a centuries-old mystery; it opened a whole new chapter in the world of mathematics. The ripple effects of his work are felt far and wide, inspiring a myriad of research avenues that delve deeper into the realms of number theory, algebraic geometry, and beyond. Imagine a pebble dropped into a calm pond, creating concentric ripples that spread outwards—this is precisely how Wiles's achievement has influenced the mathematical landscape.
One of the most significant areas of research that emerged from Wiles's proof is the study of modular forms and their connections to elliptic curves. Wiles's work showed that these two seemingly disparate areas of mathematics were intricately linked, paving the way for further exploration into their relationship. Researchers began to investigate how these connections could lead to new insights in both number theory and algebraic geometry. The implications are profound, as they not only deepen our understanding of existing theories but also challenge mathematicians to think outside the box.
Moreover, Wiles's proof has sparked a renewed interest in the Langlands Program, a set of conjectures that connect number theory and representation theory. This ambitious framework seeks to unify various branches of mathematics, and Wiles's insights have provided a fresh perspective on these complex relationships. As mathematicians dive into this program, they are uncovering new pathways that could lead to groundbreaking discoveries.
Another area of research that has gained momentum is arithmetic geometry. Wiles's techniques have inspired mathematicians to apply similar methods to tackle other longstanding problems in the field. For instance, researchers are now exploring the Birch and Swinnerton-Dyer Conjecture, which relates the number of rational points on an elliptic curve to the behavior of an associated L-function. This conjecture, like Fermat's Last Theorem, has remained unsolved for decades, and Wiles's work has provided a framework that could potentially lead to its resolution.
As a testament to the far-reaching impact of Wiles's contributions, numerous conferences and workshops have been dedicated to exploring the themes and techniques he introduced. These gatherings serve as a melting pot for ideas, where mathematicians from various backgrounds come together to share their findings and collaborate on new projects. It's a vibrant community that thrives on the inspiration derived from Wiles's monumental achievement.
In summary, the research inspired by Andrew Wiles is not just a continuation of existing mathematical inquiry; it represents a dynamic evolution of the field. His work has not only resolved a historical enigma but has also laid the groundwork for future explorations that promise to deepen our understanding of mathematics in ways we are only beginning to comprehend. As we look ahead, it’s clear that Wiles's legacy will continue to inspire generations of mathematicians, pushing the boundaries of what we know and how we think about numbers.
- What is Fermat's Last Theorem? Fermat's Last Theorem states that there are no three positive integers a, b, and c that satisfy the equation a^n + b^n c^n for any integer value of n greater than 2.
- Who is Andrew Wiles? Andrew Wiles is a British mathematician who is best known for proving Fermat's Last Theorem, a feat he accomplished in 1994 after years of intense research.
- What are modular forms? Modular forms are complex functions that are symmetric in a certain way and have applications in number theory, particularly in the study of elliptic curves.
- What is the Langlands Program? The Langlands Program is a set of conjectures and theories that propose deep connections between number theory and representation theory, aiming to unify various areas of mathematics.

Recognition and Awards
Andrew Wiles's extraordinary contributions to mathematics, particularly through his proof of Fermat's Last Theorem, have not gone unnoticed. Over the years, he has received numerous accolades that underscore the significance of his work and its impact on the mathematical community. One of the most prestigious awards he received is the Clay Millennium Prize, awarded in 1999. This prize was established to recognize outstanding contributions to the field of mathematics, and Wiles's achievement in proving a theorem that had puzzled mathematicians for over 350 years certainly qualified him for this honor.
In addition to the Clay Millennium Prize, Wiles has been honored with several other awards throughout his career. These include the Royal Medal from the Royal Society in 2005 and the Abel Prize in 2016, which is often considered one of the highest distinctions in mathematics. The Abel Prize is awarded annually by the King of Norway to one or more outstanding mathematicians, and Wiles received it for his groundbreaking work that not only proved Fermat's Last Theorem but also opened new pathways in number theory.
Moreover, Wiles has been elected as a fellow of several esteemed organizations, including the American Academy of Arts and Sciences and the Royal Society of London. His election to these organizations is a testament to his influence and the high regard in which he is held by his peers. Each accolade he has received is not just a personal achievement but also a recognition of the profound implications his work has had on the field of mathematics.
To illustrate the breadth of Wiles's recognition, here is a table summarizing some of the key awards and honors he has received:
| Award | Year | Organization |
|---|---|---|
| Clay Millennium Prize | 1999 | Clay Mathematics Institute |
| Royal Medal | 2005 | Royal Society |
| Abel Prize | 2016 | Norwegian Academy of Science and Letters |
Wiles's journey does not end with these accolades; his work continues to inspire a new generation of mathematicians. The recognition he has received serves as a beacon for aspiring mathematicians, showing that dedication, perseverance, and a passion for solving the unsolvable can lead to groundbreaking discoveries. His story is a reminder that while the path of mathematics can be filled with challenges, the rewards of intellectual exploration and discovery are immeasurable.
- What is Fermat's Last Theorem? Fermat's Last Theorem states that there are no three positive integers a, b, and c that satisfy the equation an + bn cn for any integer value of n greater than 2.
- How long did it take Andrew Wiles to prove the theorem? Wiles worked on the proof for nearly seven years, from 1986 to 1993, before finally presenting it in 1994.
- What are elliptic curves and modular forms? Elliptic curves are a type of smooth, projective algebraic curve, while modular forms are complex functions that are analytic and exhibit a certain kind of symmetry. Both concepts played a crucial role in Wiles's proof.
Frequently Asked Questions
- What is Fermat's Last Theorem?
Fermat's Last Theorem states that there are no three positive integers a, b, and c that satisfy the equation an + bn cn for any integer value of n greater than 2. This theorem puzzled mathematicians for over 350 years until Andrew Wiles proved it in 1994, marking a monumental achievement in number theory.
- Why is Andrew Wiles's proof significant?
Wiles's proof of Fermat's Last Theorem is significant because it not only solved a longstanding mathematical mystery but also introduced new techniques and concepts in number theory, particularly the use of elliptic curves and modular forms. This breakthrough has since opened up new avenues for research and has inspired countless mathematicians.
- What challenges did Wiles face during his proof?
Wiles faced numerous challenges while proving Fermat's Last Theorem, including initial setbacks and the complexity of the mathematics involved. He worked in secrecy for several years, only to discover a flaw in his proof shortly before its announcement. However, with determination and creativity, he was able to rectify the issues and ultimately succeed.
- How did Wiles's early life influence his work?
Andrew Wiles's early life played a crucial role in shaping his passion for mathematics. Growing up, he was captivated by the beauty and challenges of mathematical problems. His education, particularly at the University of Cambridge, provided him with a strong foundation and the inspiration needed to pursue his groundbreaking work in number theory.
- What are elliptic curves and modular forms?
Elliptic curves are algebraic curves defined by cubic equations, which have important implications in number theory. Modular forms are complex functions that are invariant under certain transformations and have deep connections to number theory. Wiles's proof utilized these concepts to establish a link between them, which was key to proving Fermat's Last Theorem.
- What impact did Wiles's proof have on mathematics?
Wiles's proof had a profound impact on mathematics, particularly in number theory. It not only resolved a historic problem but also inspired new research directions and methodologies. Mathematicians continue to explore the ideas introduced by Wiles, leading to advancements in various fields, including algebraic geometry and arithmetic.
- What recognition has Andrew Wiles received for his work?
Andrew Wiles has received numerous accolades for his contributions to mathematics, including the prestigious Abel Prize in 2016 and the Chern Medal in 2018. His work has not only earned him recognition within the mathematical community but also brought mathematics into the public spotlight, showcasing its beauty and significance.
- How can I learn more about Wiles's work?
If you're interested in learning more about Andrew Wiles's work and Fermat's Last Theorem, there are many resources available, including books, documentaries, and academic papers. A great starting point is Wiles's own publications or popular science books that explain his proof in an accessible manner.



















